B.tech 1st SEM

Unit1

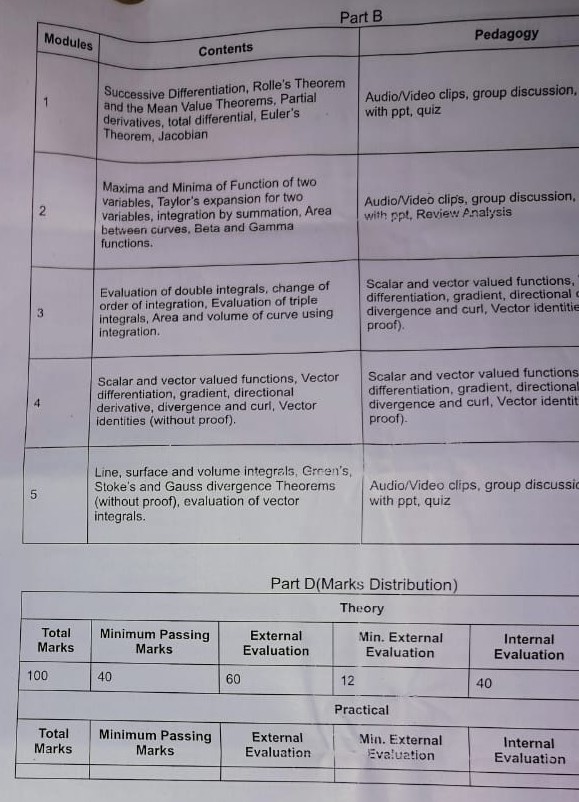
Differentiation, Extrema on an Interval, Rolle’s Theorem and the Mean Value Theorem, Increasing and Decreasing

Functions and First derivative test, Second derivative test, Maxima and Minima.

Functions of two variables, partial derivatives, total differential, Jacobian and it Prosperities

Unit2

Taylor’s expansion for two variables, maxima and minima, constrained maxima and minima, Lagrange’s multiplier method. Integration, Average function value, Area between curves, Volumes of solids of revolution, Beta and Gamma functions, interrelation.

Unit3

Evaluation of double integrals, change of order of integration, change of variables between Cartesian and polar co-ordinates, Evaluation of triple integrals, change of variables between Cartesian and cylindrical and spherical co-ordinates, evaluation of multiple integrals using gamma and beta functions.

Unit4

Scalar and vector valued functions, gradient, tangent plane, directional derivative, divergence and curl, scalar and vector potentials, Statement of vector identities, Simple problems.

Unit5

Line, surface and volume integrals, Statement of Green’s, Stoke’s and Gauss divergence Theorems, verification and evaluation of vector integrals using them.